6 Altitude Adjustment
We have a survey open right now that we invite you to fill out.
Blood flow to the brain is regulated by the concentration of CO2 and O2 in the blood, as well as blood pressure, and these factors change at high altitude. Thinner air leads to decreased O2 in the blood, resulting in the dilation of brain blood vessels and thus increased blood flow. At the same time, increased breathing due to thin air leads to lower blood CO2 and constriction of blood vessels, so results in decreased blood brain flow.
With these conflicting signals, what is the end result? This lesson investigates this effect of altitude on blood flow to the brain, as well as how the factors that influence blood brain flow change across time.
Data was collected by a research team from the University of Otago who travelled to Nepal in 2008, and this is presented by Sam Lucas (Physiology Dept., University of Otago).
Data
There is 1 file associated with this presentation. It contains the data you will need to complete the lesson tasks.
Video
Objectives
Tasks
This data was collected to investigate the effects of living at high altitude. A cohort of 17 people were first measured at sea level, then again in the Himalayas over two weeks of living at high altitude (5050m). All in the cohort were measured at Days 1-3 at high altitude, and 12 of the people were measured at Days 7-9 and again at Days 12-15.
0. Read and Format data
0a. Read in the data
First check you have installed the package readxl (see Section 2.6) and set the working directory (see Section 2.1), using instructions in Getting started with R.
"Sheet2" contains a reformatted version of the data that will be easier to handle in R. We also specify the range= " " of cells to include in each input to create one data frame for each of the physiological markers Brain blood Flow and PaO2/PaCO2.
Load the data into R, specifying "Sheet2" and the appropriate range= " " of the data.
Code
#loads readxl package
library(readxl)
#loads the data file and names it brainblood
brainblood<-read_xls("brain blood flow.xls",sheet="Sheet2",range="A2:I19")
#view beginning of data frame
head(brainblood)
#loads the data file and names it paO2paCO2
paO2paCO2<-read_xls("brain blood flow.xls",sheet="Sheet2",range="A23:I40")
head(paO2paCO2)Code
#loads readxl package
library(readxl) Warning: package 'readxl' was built under R version 4.2.2Code
#loads the data file and names it brainblood
brainblood<-read_xls("brain blood flow.xls",sheet="Sheet2",range="A2:I19")
#view beginning of data frame
head(brainblood) # A tibble: 6 × 9
`PP #` Baseline `D1-3` `D7-9` `D12-15` DiffBaseline1…¹ PDiff…² PDiff…³ PDiff…⁴
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 50.1 70.3 56.3 67.8 20.2 40.4 12.3 35.2
2 2 82.6 112. 83.3 76.7 29.7 36.0 0.901 -7.13
3 3 50.1 67.5 57.2 50.6 17.4 34.7 14.1 0.929
4 4 62.8 68.3 69.6 70.2 5.49 8.74 10.9 11.9
5 5 80.5 77.5 67.8 74.0 -3.01 -3.73 -15.8 -8.09
6 6 80.9 72.3 72.9 74.2 -8.56 -10.6 -9.93 -8.24
# … with abbreviated variable names ¹`DiffBaseline1-3`, ²`PDiffBaseline1-3`,
# ³`PDiffBaselineD7-9`, ⁴`PDiffBaselineD12-15`Code
#loads the data file and names it paO2paCO2
paO2paCO2<-read_xls("brain blood flow.xls",sheet="Sheet2",range="A23:I40")
head(paO2paCO2)# A tibble: 6 × 9
`PP #` Baseline `D1-3` `D7-9` `D12-15` DiffBaseline1…¹ PDiff…² PDiff…³ PDiff…⁴
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 2.41 1.8 1.92 1.74 -0.610 -25.3 -20.3 -27.8
2 2 2.56 1.48 1.71 1.88 -1.08 -42.2 -33.1 -26.5
3 3 2.51 1.34 1.6 1.66 -1.17 -46.5 -36.3 -34.1
4 4 2.87 1.88 1.27 1.8 -0.988 -34.5 -55.8 -37.2
5 5 2.39 1.68 1.62 1.78 -0.712 -29.8 -32.2 -25.6
6 6 2.02 1.42 1.62 1.48 -0.604 -29.9 -19.9 -26.8
# … with abbreviated variable names ¹`DiffBaseline1-3`, ²`PDiffBaseline1-3`,
# ³`PDiffBaseline7-9`, ⁴`PDiffBaseline12-15`The brain blood flow variables contain measurements of the rate of blood flow in cm/s, and the blood gas variables contain measurements of the ratio of oxygen to carbon dioxide in the blood.
The data frame for each physiological marker contains the same 9 variables. PP# numbers the participants in the study and Baseline gives the first measurement taken at sea level. D1-3, D7-9, and D12-15 give the measurements taken at high altitude days 1 to 3, 7 to 9 and 12 to 15 respectively. DiffBaseline1-3 gives the absolute difference between measurements at sea level and day 1 to 3. PDiffBaseline1-3 gives the percentage difference between sea level and day 1 to 3 measurements, with this percentage difference also provided for day 7 to 9 and 12 to 15 measurements by the variables PDiffBaselineD7-9 and PDiffBaselineD12-15.
1. Strip Chart
Plot the blood brain flow data against the stage of the trial (Baseline, D1-3, D7-9, and D12-15) using the function stripchart().
What pattern can you see from the graph?
Since our y variable is continuous (rather than discrete) we will have many points that are close together on the graph but not exactly the same values. To separate points for easier interpretation we use method="jitter". You can adjust the jitter= value to see how this changes the output.
Code
#we only want to plot the variables in columns 2 to 5, so we subset this section of the data frame.
#vertical=T changes the orientation of the plot.
stripchart(x=brainblood[,2:5],method="jitter",jitter=0.075,vertical=T) Code
#we only want to plot the variables in columns 2 to 5, so we subset this section of the data frame.
#vertical=T changes the orientation of the plot.
stripchart(x=brainblood[,2:5],method="jitter",jitter=0.075,vertical=T) 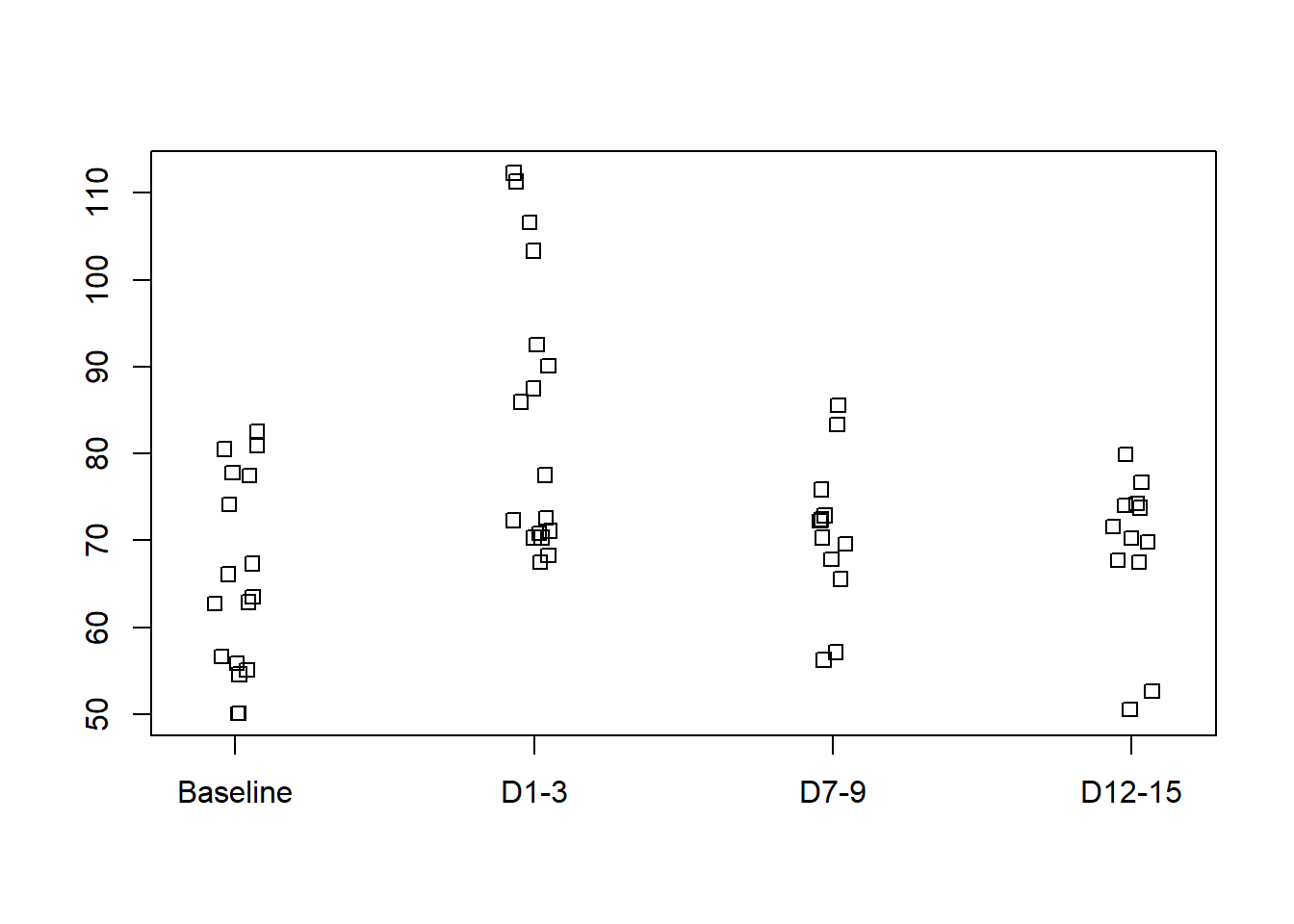
The rate of blood flow is fastest on high altitude days 1-3, while for days 7-9 and 12-15 it appears to return to baseline rates.
2. Practice: Strip Chart
Try plotting the blood gas ratio data against the stage of the trial. Explore some different pch= and col= combinations to create an attractive plot (you can google to see the options).
What do you observe?
Code
stripchart(x=paO2paCO2[,2:5],method="jitter",jitter=0.075,vertical=T,pch=20,col="turquoise3")Code
stripchart(x=paO2paCO2[,2:5],method="jitter",jitter=0.075,vertical=T,pch=20,col="turquoise3")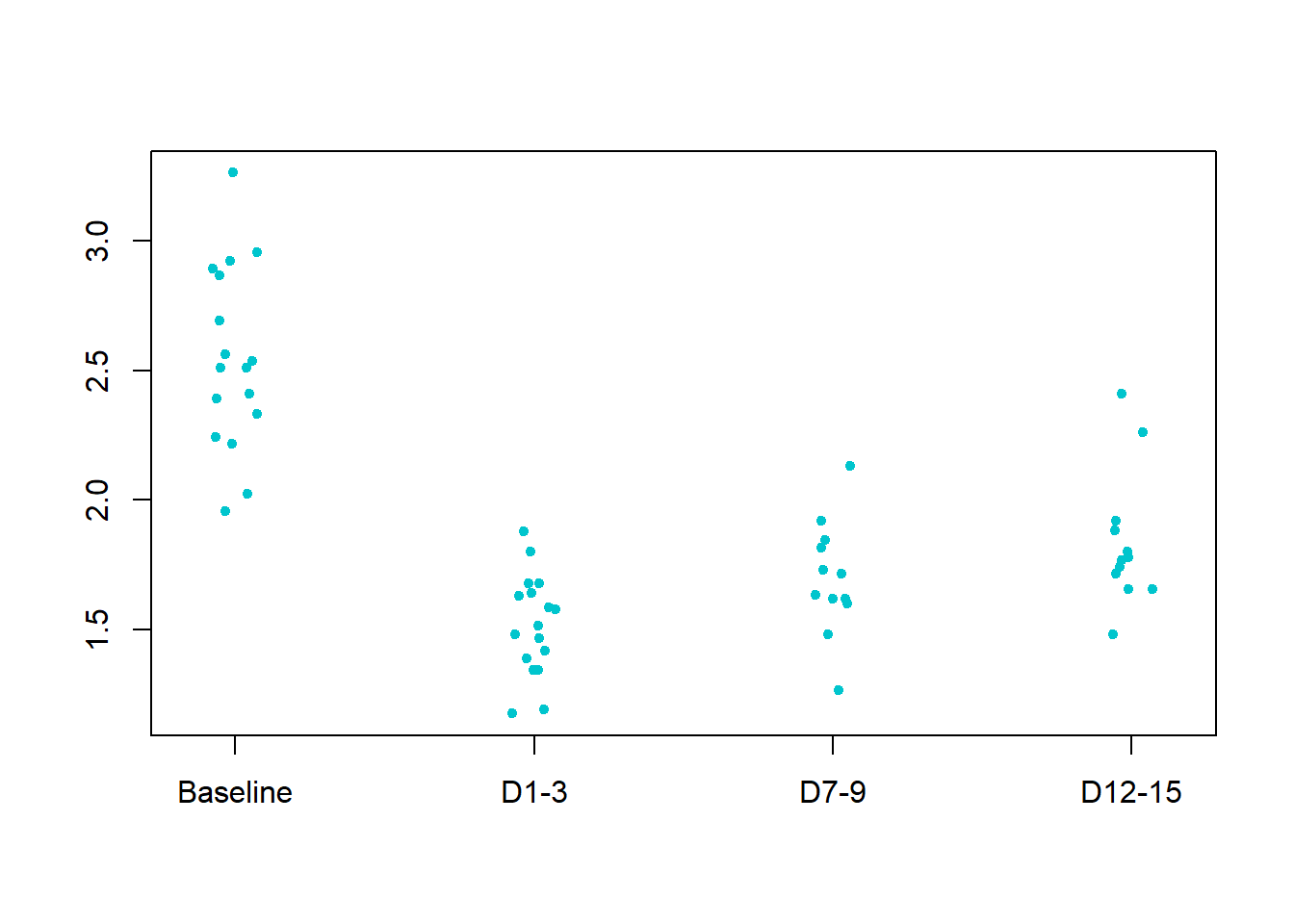
The ratio of oxygen to carbon dioxide in the blood drops considerably from baseline on days 1-3 at high altitude. It then increases slightly on days 5-7 and again on days 12-15, but is still lower than baseline levels.
3. Confidence Interval, Hypothesis Test (mean difference)
Investigate if there is a significant difference between the brain blood flow measures at Baseline and after days 1-3 at high altitude (D1-3), by setting up the 95% confidence interval for the mean difference.
The easiest way to assess whether there is a mean difference is to use a paired t.test(). Have a think about why we treat the data as paired/matched this time rather than as two separate samples.
What do you conclude from the confidence interval?
Code
#first test if variances are equal
var.test(brainblood$`D1-3`,brainblood$Baseline, alternative = "two.sided")
#no significant evidence against null hypothesis that variances are equal, use var.equal=T in t test
t.test(brainblood$`D1-3`,brainblood$Baseline,var.equal = T,paired=T)Code
#first test if variances are equal
var.test(brainblood$`D1-3`, brainblood$Baseline,alternative = "two.sided")
F test to compare two variances
data: brainblood$`D1-3` and brainblood$Baseline
F = 2.0352, num df = 16, denom df = 16, p-value = 0.166
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.7370435 5.6200332
sample estimates:
ratio of variances
2.035242 Code
#no significant evidence against null hypothesis that variances are equal, use var.equal=T in t test
t.test(brainblood$`D1-3`,brainblood$Baseline,var.equal = T,paired=T)
Paired t-test
data: brainblood$`D1-3` and brainblood$Baseline
t = 4.2575, df = 16, p-value = 0.0006017
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
9.211434 27.482155
sample estimates:
mean difference
18.34679 The t-test is equivalent to considering whether zero is in the confidence interval for the mean difference (null hypothesis is that true difference is zero), and a ‘large’ test statistic suggests that this difference is not equal to zero (alternative hypothesis). To assess whether this is ‘large’ enough, we look at the probability value, and if it is less than 0.05 (for a test equivalent to using a 95% confidence interval), then we conclude that there is indeed a mean difference, as is the case here. The associated confidence interval is entirely positive, so we can be 95% confident that the true mean difference in blood flow rate is between 9.211 and 27.482 cm/s faster on days 1-3 at high altitude compared to baseline.
Modify the code to calculate t.test() confidence intervals investigating whether there is a difference in brain blood flow at Baseline and at altitude after some acclimatisation (D7-9), and whether there is a difference at Baseline and at altitude after more acclimatisation (D12-15).
Report your findings.
For a further extension use the blood gas data to calculate a t.test() confidence interval for the difference between Baseline measurements at sea level and the altitude measurements (for D1-3).
Report your findings.
4. Bootstrap Confidence Interval, Histogram (mean)
Using the provided data, estimate the distribution of the mean difference in brain blood flow at Baseline and at D1-3 by bootstrapping the mean for DiffBaseline1-3. Using this distribution, provide a new estimate of the mean difference along with a 95% confidence interval for it.
To perform this, we use the bootstrap technique. This involves randomly sampling a new dataset from the original sampled data. By doing this several times, we create a large number of datasets that we might have seen had we performed the experiment multiple times. By computing the mean for each of these datasets, we get an estimate of the distribution of the statistic.
What distribution do the bootstrapped estimates of the mean appear to have?
How does the bootstrap estimate of the mean difference compare to the previous estimate?
Does the bootstrap confidence interval lead to the same conclusion as before? Could we have expected this?
Code
library(boot)
#set seed so you get the same results when running again
set.seed(40)
#function that calculates the mean from the bootstrapped samples
meanFun<-function(data,indices){
dataInd<-data[indices,]
meandata<-mean(dataInd$`DiffBaseline1-3`,na.rm=T)
return(meandata)
}
#bootstrap difference in mean blood flow at baseline and days 1-3.
#Create object called meanBoot with the output of the bootstrapping procedure
meanBoot<-boot(brainblood,statistic=meanFun, R=10000) We can then have a look at the results from our bootstrap, particularly the \(\verb!original!\) column which gives the estimated mean difference.
Code
#view bootstrap output
meanBoot We can also automatically calculate our 95% confidence interval using boot.ci(). The code below calculates a percentile interval, but you can change the type= " " to compare different intervals.
Code
#percentile confidence interval
percCi<-boot.ci(meanBoot,type="perc")
#check lower and upper limits from percentile interval object
percCi$percent[4:5] We can plot the distribution of bootstrapped mean differences, with a density curve and 95% percentile confidence interval limits on top.
In the hist() function, you can use breaks= to change the number of bars. Make the density curve and confidence interval limits distinct from the histogram underneath, you can do this by using a combination of col= (colour), lwd= (line width) and lty= (line type) arguments when adding these components.
Code
#plot density histogram of bootstrap results
hist(meanBoot$t,breaks=12,freq=F)
#add a smoothed line to show the distribution
lines(density(meanBoot$t),col="red4",lwd=2)
#ci limits
abline(v=percCi$percent[4:5],col="red3",lty=2)Code
library(boot)Warning: package 'boot' was built under R version 4.2.2Code
#set seed so you get the same results when running again
set.seed(40)
#function that calculates the mean from the bootstrapped samples
meanFun<-function(data,indices){
dataInd<-data[indices,]
meandata<-mean(dataInd$`DiffBaseline1-3`,na.rm=T)
return(meandata)
}
#bootstrap difference in mean blood flow at baseline and days 1-3.
#Create object called meanBoot with the output of the bootstrapping procedure
meanBoot<-boot(brainblood,statistic=meanFun, R=10000) We can then have a look at the results from our bootstrap, particularly the \(\verb!original!\) column which gives the estimated mean difference.
Code
#view bootstrap output
meanBoot
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = brainblood, statistic = meanFun, R = 10000)
Bootstrap Statistics :
original bias std. error
t1* 18.34679 -0.01070167 4.145039We can also automatically calculate our 95% confidence interval using boot.ci(). The code below calculates a percentile interval, but you can change the type= " " to compare different intervals.
Code
#percentile confidence interval
percCi<-boot.ci(meanBoot,type="perc")
#check lower and upper limits from percentile interval object
percCi$percent[4:5] [1] 10.48971 26.65469We can plot the distribution of bootstrapped mean differences, with a density curve and 95% percentile confidence interval limits on top.
In the hist() function, you can use breaks= to change the number of bars. Make the density curve and confidence interval limits distinct from the histogram underneath, you can do this by using a combination of col= (colour), lwd= (line width) and lty= (line type) arguments when adding these components.
Code
#plot density histogram of bootstrap results
hist(meanBoot$t,breaks=12,freq=F)
#add a smoothed line to show the distribution
lines(density(meanBoot$t),col="red4",lwd=2)
#ci limits
abline(v=percCi$percent[4:5],col="red3",lty=2)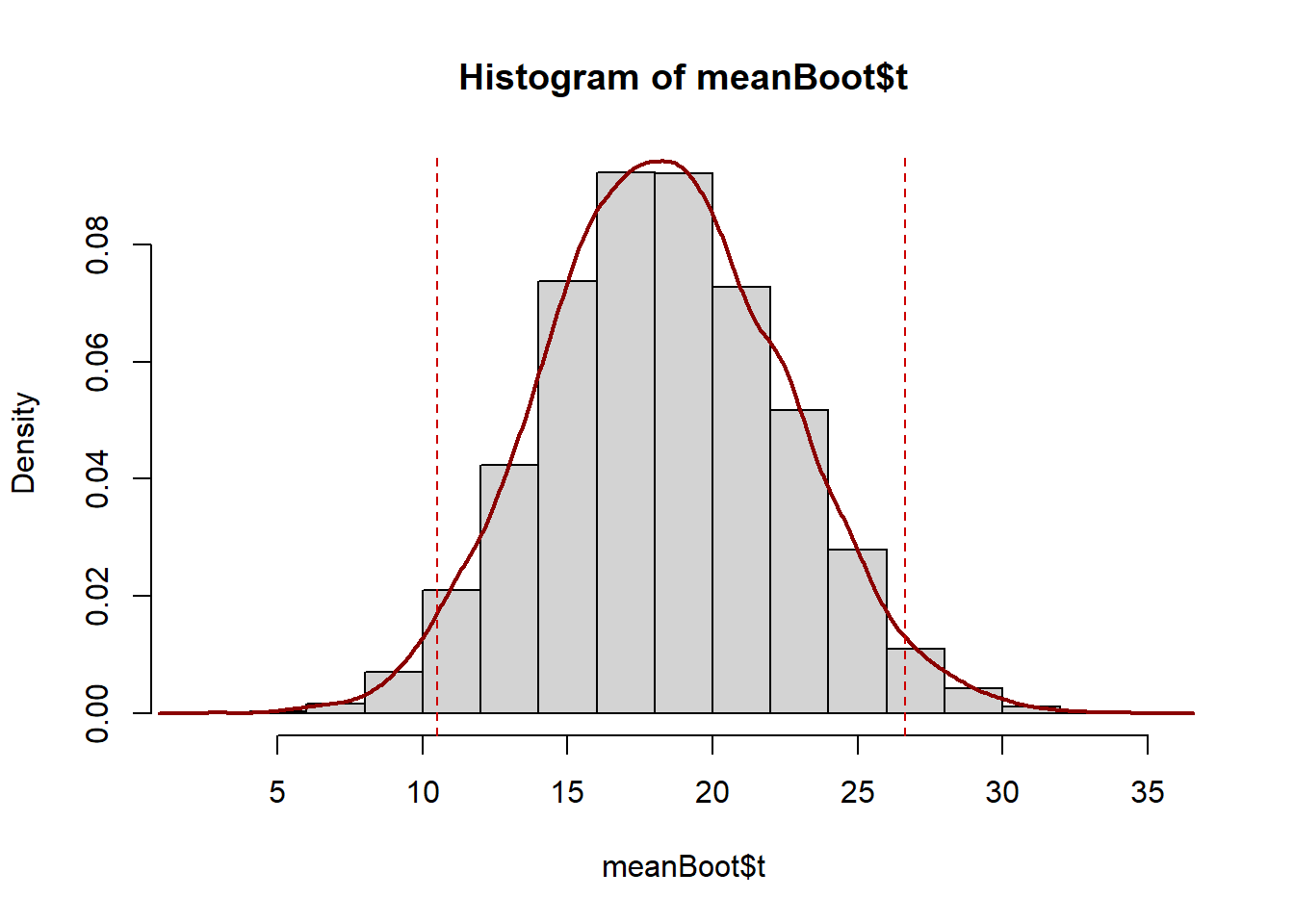
The bootstrapped means for the (paired) mean difference between baseline and days 1-3 follows a normal distribution symmetric around a mean of 18.34679. This mean of mean differences matches the mean difference in days 1-3 and baseline blood flow rate we calculated earlier, and the distribution of bootstrapped mean difference estimates around it give an indication of the amount of variability in our estimate due to sampling.
The bootstrap confidence interval is slightly narrower than the one calculated earlier and includes only positive values so leads to the same conclusion. There is significant evidence to conclude a mean difference in blood flow rate between baseline and days 1-3 at high altitude.
As the earlier confidence interval was well above 0 (lower limit of 9.211434) and bootstrap confidence intervals only differ slightly from those calculated by hand or t.test() this outcome is fairly unsurprising. We would not expect the bootstrap confidence interval to differ so dramatically that 0 was included.
Modify the code to calculate bootstrap confidence intervals investigating whether there is a difference in brain blood flow at Baseline and at altitude after some acclimatisation (D7-9), and whether there is a difference at Baseline and at altitude after more acclimatisation (D12-15).
Report your findings.
For a further extension use the blood gas data to calculate the bootstrap confidence interval for the difference between Baseline measurements at sea level and the altitude measurements (for D1-3).
Report your findings.
